It's a secret to no one that maths is hard, so when you start talking about the hardest maths problems ever, things start to get a little crazy. Take the innocuously named Question 6, which is so complex, it can bring mathematicians to tears.
As mathematician Simon Pampena explains the Numberphile video above, the Legend of Question 6 spawned from a maths competition for high-schoolers held in Australia in 1988. (Yep, they make 'em tough down here.)
The competition was the International Mathematical Olympiad, which is held every year in a different country, and only six kids from every country are selected to compete. Points are scored on how each 'mathlete' performs on six different questions.
In 1988, the Australian Olympiad officials decided to throw a massive curveball to the kids on the final day of competition, and it's gone down in history as one of the toughest problems out there.
Just to give you an idea of how tough it was, Australian-American mathematician Terence Tao - recipient of the 2006 Fields Medal (the mathematician's 'Nobel Prize') - scored a 1 out of 7 when he attempted it. But, you know, he was 13 at the time, so let's cut the man some slack.
What made Question 6 so hard is that it actually tried to pay mind games with you as you solved it.
"In a way, they're actually designed to kind of throw you off if you know high school maths too well," says Pampena. "So say if you really know how to solve quadratic equations, and you see something that looks like a quadratic equation, it almost throws you down the wrong path."
Question 6 was actually submitted to the Australian Olympiad officials by a mathematician from West Germany, and the officials gave themselves SIX HOURS to solve it to see if it should be included in the event.
Not one official could solve Question 6 within the time limit. Some of the best mathematicians in the world at the time.
But they put it on a test for kids anyway, and only gave them about 90 minutes to solve it, because mathematicians are ridiculous.
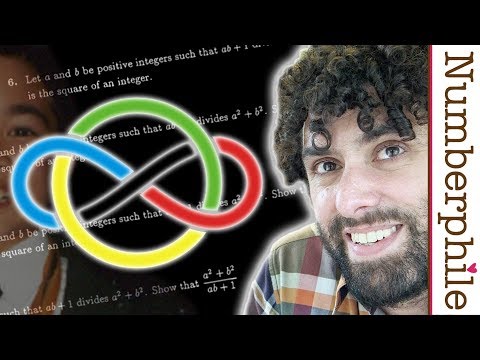
So you just want to know wtf this problem is, right? Okay, here it is:
Let a and b be positive integers such that ab + 1 divides a2 + b2. Show that a2 + b2 / ab + 1 is the square of an integer.
What's the solution? Well, we're going to let the Numberphile video above explain that one to you… nope sorry, there's no way they're fitting all that into a single video.
The video above will tell you what the question actually means, and then the video below will give you the answer:

Just please don't pop a vein in your head or something if you attempt it yourself. And if you somehow crush it, here's six more to try.
Good luck…
