How a Genius Formula Carved Onto a Bridge Changed Mathematical History

On October 16 1843, the Irish mathematician William Rowan Hamilton had an epiphany during a walk alongside Dublin's Royal Canal. He was so excited he took out his penknife and carved his discovery right then and there on Broome Bridge.

It is the most famous graffiti in mathematical history, but it looks rather unassuming:

i ² = j ² = k ² = -1

Yet Hamilton's revelation changed the way mathematicians represent information. And this, in turn, made myriad technical applications simpler – from calculating forces when designing a bridge, an MRI machine or a wind turbine, to programming search engines and orienting a rover on Mars.

So, what does this famous graffiti mean?

Rotating objects

The mathematical problem Hamilton was trying to solve was how to represent the relationship between different directions in three-dimensional space. Direction is important in describing forces and velocities, but Hamilton was also interested in 3D rotations.

Mathematicians already knew how to represent the position of an object with coordinates such as x, y and z, but figuring out what happened to these coordinates when you rotated the object required complicated spherical geometry. Hamilton wanted a simpler method.

He was inspired by a remarkable way of representing two-dimensional rotations.

The trick was to use what are called "complex numbers", which have a "real" part and an "imaginary" part. The imaginary part is a multiple of the number i, "the square root of minus one", which is defined by the equation i ² = –1.

By the early 1800s several mathematicians, including Jean Argand and John Warren, had discovered that a complex number can be represented by a point on a plane. Warren had also shown it was mathematically quite simple to rotate a line through 90° in this new complex plane, like turning a clock hand back from 12.15pm to 12 noon. For this is what happens when you multiply a number by i.

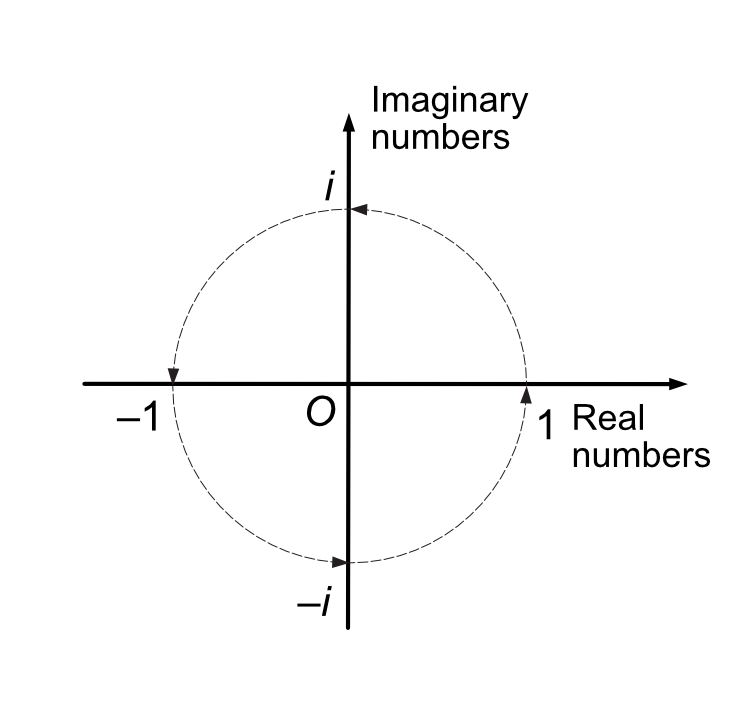
Hamilton was mightily impressed by this connection between complex numbers and geometry, and set about trying to do it in three dimensions. He imagined a 3D complex plane, with a second imaginary axis in the direction of a second imaginary number j, perpendicular to the other two axes.

It took him many arduous months to realise that if he wanted to extend the 2D rotational wizardry of multiplication by i he needed four-dimensional complex numbers, with a third imaginary number, k.

In this 4D mathematical space, the k-axis would be perpendicular to the other three. Not only would k be defined by k ² = –1, its definition also needed k = ij = –ji. (Combining these two equations for k gives ijk = –1.)

Putting all this together gives i ² = j ² = k ² = ijk = –1, the revelation that hit Hamilton like a bolt of lightning at Broome Bridge.

Quaternions and vectors

Hamilton called his 4D numbers "quaternions", and he used them to calculate geometrical rotations in 3D space. This is the kind of rotation used today to move a robot, say, or orient a satellite.

But most of the practical magic comes into it when you consider just the imaginary part of a quaternion. For this is what Hamilton named a "vector".

A vector encodes two kinds of information at once, most famously the magnitude and direction of a spatial quantity such as force, velocity or relative position. For instance, to represent an object's position (x, y, z) relative to the "origin" (the zero point of the position axes), Hamilton visualised an arrow pointing from the origin to the object's location. The arrow represents the "position vector" x i + y j + z k.

This vector's "components" are the numbers x, y and z – the distance the arrow extends along each of the three axes. (Other vectors would have different components, depending on their magnitudes and units.)

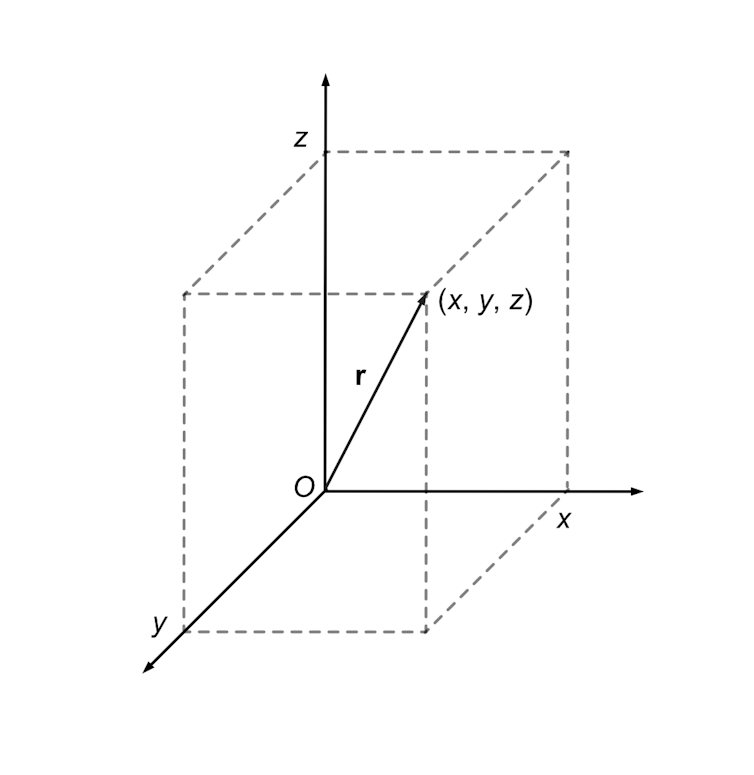
Half a century later, the eccentric English telegrapher Oliver Heaviside helped inaugurate modern vector analysis by replacing Hamilton's imaginary framework i, j, k with real unit vectors, i, j, k. But either way, the vector's components stay the same – and therefore the arrow, and the basic rules for multiplying vectors, remain the same, too.

Hamilton defined two ways to multiply vectors together. One produces a number (this is today called the scalar or dot product), and the other produces a vector (known as the vector or cross product). These multiplications crop up today in a multitude of applications, such as the formula for the electromagnetic force that underpins all our electronic devices.

A single mathematical object

Unbeknown to Hamilton, the French mathematician Olinde Rodrigues had come up with a version of these products just three years earlier, in his own work on rotations. But to call Rodrigues' multiplications the products of vectors is hindsight. It is Hamilton who linked the separate components into a single quantity, the vector.

Everyone else, from Isaac Newton to Rodrigues, had no concept of a single mathematical object unifying the components of a position or a force. (Actually, there was one person who had a similar idea: a self-taught German mathematician named Hermann Grassmann, who independently invented a less transparent vectorial system at the same time as Hamilton.)

Hamilton also developed a compact notation to make his equations concise and elegant. He used a Greek letter to denote a quaternion or vector, but today, following Heaviside, it is common to use a boldface Latin letter.

This compact notation changed the way mathematicians represent physical quantities in 3D space.

Take, for example, one of Maxwell's equations relating the electric and magnetic fields:

With just a handful of symbols (we won't get into the physical meanings of ∂/∂t and ∇ ×), this shows how an electric field vector (E) spreads through space in response to changes in a magnetic field vector (B).

Without vector notation, this would be written as three separate equations (one for each component of B and E) – each one a tangle of coordinates, multiplications and subtractions.

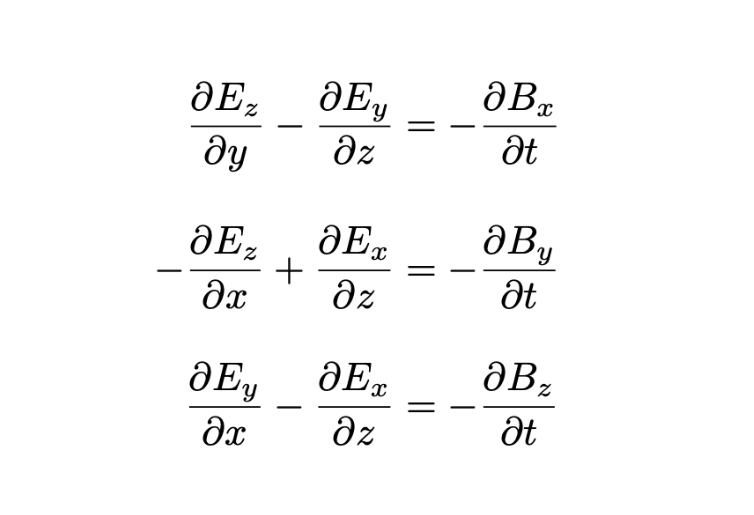
The power of perseverance

I chose one of Maxwell's equations as an example because the quirky Scot James Clerk Maxwell was the first major physicist to recognise the power of compact vector symbolism. Unfortunately, Hamilton didn't live to see Maxwell's endorsement. But he never gave up his belief in his new way of representing physical quantities.

Hamilton's perseverance in the face of mainstream rejection really moved me, when I was researching my book on vectors. He hoped that one day – "never mind when" – he might be thanked for his discovery, but this was not vanity. It was excitement at the possible applications he envisaged.

He would be over the Moon that vectors are so widely used today, and that they can represent digital as well as physical information. But he'd be especially pleased that in programming rotations, quaternions are still often the best choice – as NASA and computer graphics programmers know.

In recognition of Hamilton's achievements, maths buffs retrace his famous walk every October 16 to celebrate Hamilton Day. But we all use the technological fruits of that unassuming graffiti every single day.

Robyn Arianrhod, Affiliate, School of Mathematics, Monash University

This article is republished from The Conversation under a Creative Commons license. Read the original article.