If you studied algebra in high school (or you're learning it right now), there's a good chance you're familiar with the quadratic formula. If not, it's possible you repressed it.
By this point, billions of us have had to learn, memorise, and implement this unwieldy algorithm in order to solve quadratic equations, but according to mathematician Po-Shen Loh from Carnegie Mellon University, there's actually been an easier and better way all along, although it's remained almost entirely hidden for thousands of years.
In a 2019 research paper, Loh celebrates the quadratic formula as a "remarkable triumph of early mathematicians" dating back to the beginnings of the Old Babylonian Period around 2000 BCE, but also freely acknowledges some of its ancient shortcomings.
"It is unfortunate that for billions of people worldwide, the quadratic formula is also their first (and perhaps only) experience of a rather complicated formula which they must memorise," Loh writes.
That arduous task – performed by approximately four millennia worth of maths students, no less – may not have been entirely necessary, as it happens. Of course, there have always been alternatives to the quadratic formula, such as factoring, completing the square, or even breaking out the graph paper.
But the quadratic formula is generally regarded as the most comprehensive and reliable method for solving quadratic problems, even if it is a bit inscrutable. This is what it looks like:
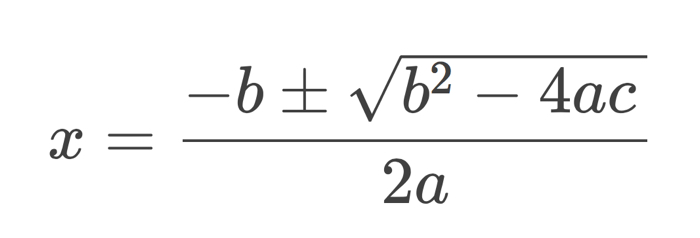
That formula can be used to solve standard form quadratic equations, where ax2 + bx + c = 0.
In September 2019, Loh was brainstorming the mathematics behind quadratic equations when he struck upon a new, simplified way of deriving the same formula – an alternative method which he describes in his paper as a "computationally-efficient, natural, and easy-to-remember algorithm for solving general quadratic equations".
"I was dumbfounded," Loh says of the discovery. "How can it be that I've never seen this before, and I've never seen this in any textbook?"
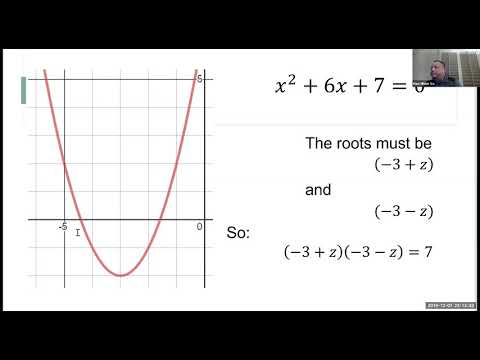
In Loh's new method, he starts from the standard method of trying to factor the quadratic x² + bx + c as (x − )(x − ), which amounts to looking for two numbers to put in the blanks with sum −b and product c. He uses an averaging technique that concentrates on the sum, as opposed to the more commonly taught way of focusing on the product of two numbers that make up c, which requires guesswork to solve problems.
"The sum of two numbers is 2 when their average is 1." Loh explains on his website.
"So, we can try to look for numbers that are 1 plus some amount, and 1 minus the same amount. All we need to do is to find if there exists a u such that 1 + u and 1 − u work as the two numbers, and u is allowed to be 0."
According to Loh, a valid value for u can always be determined per Loh's alternative quadratic method, in an intuitive way, making it possible to solve any quadratic equation.
In Loh's paper, he admits he would "be very surprised if this approach has entirely eluded human discovery until the present day, given the 4,000 years of history on this topic", but says the alternative technique – which combines steps pioneered by Babylonian, Greek, and French mathematicians – is "certainly not widely taught or known (the author could find no evidence of it in English sources)".
However, since first sharing his pre-print paper describing the simple proof online in October, Loh says his attention has been drawn to a 1989 research article that is the most similar previous work he has found – going some way to justify his disbelief that this alternative method had not been identified before now.
"The other work overlapped in almost all calculations, with an apparent logical difference in assuming that every quadratic can be factored, and a pedagogical difference in choice of sign," Loh explained to ScienceAlert in an email.
All that remains to be solved then, is the mystery of why this technique hasn't become more widely known previous to this, since it gives us, in Loh's words, "a delightful alternative approach for solving quadratic equations, which is practical for integration into all mainstream curricula".
(Not to mention, of course, that it might just mean that nobody need ever again memorise the quadratic formula.)
We still don't know how this escaped wider notice for millennia, but if Loh's instincts are right, maths textbooks could be on the verge of a historic rewriting - and we don't take textbook-changing discoveries lightly.
"I wanted to share it as widely as possible with the world," Loh says, "because it can demystify a complicated part of maths that makes many people feel that maybe maths is not for them."
The research paper is available at pre-print website arXiv.org, and you can read Po-Shen Loh's generalised explanation of the simple proof here.
A version of this article was first published in December 2019.
