Scientists have discovered an unexpectedly simple formula that governs one of the most seemingly unknowable limits in physics: determining how much of an electric field a water droplet can withstand before it will burst.
This infinitesimal phenomenon has been studied by physicists for decades, but while the overall concept may be easy to imagine, discerning the mathematical relationships that underpin such electrified explosions has been anything but.
Now that it's been figured out, scientists say this one formula could lead to new advancements in everything from space propulsion to mass spectrometry, high-resolution printing, air purification, molecular analysis, and more.
A water droplet, bursting at its apex, due to an increasingly strong electric field. (MIT)
"Before our result, engineers and scientists had to perform computationally intensive simulations to assess the stability of an electrified droplet," explains mechanical engineering and physics graduate student Justin Beroz from MIT.
"With our equation, one can predict this behaviour immediately, with a simple paper-and-pencil calculation."
It's not something non-physicists spend a lot of time thinking about, but the phenomenon Beroz and his team have characterised in their new paper is something that takes place all the time in the real world, even if it's mostly invisible to people.
It happens when raindrops fall through the sky and are affected by the electric fields generated by storm clouds, or if they're exposed to electric fields from other sources, such as power lines.
When this occurs, the surface tension that holds water molecules together in a contained spherical form can lose its hold on the H2O, with the electrical field effectively pulling outward on the droplet as charge builds up on its surface.
In recent times, behaviours like this have been leveraged by microfluidics researchers to manipulate and move droplets around with electrical fields, but scientists still had no easy way of calculating the stability limit: the theoretical threshold where droplets of water either remain whole or burst in response to such electrical stresses.
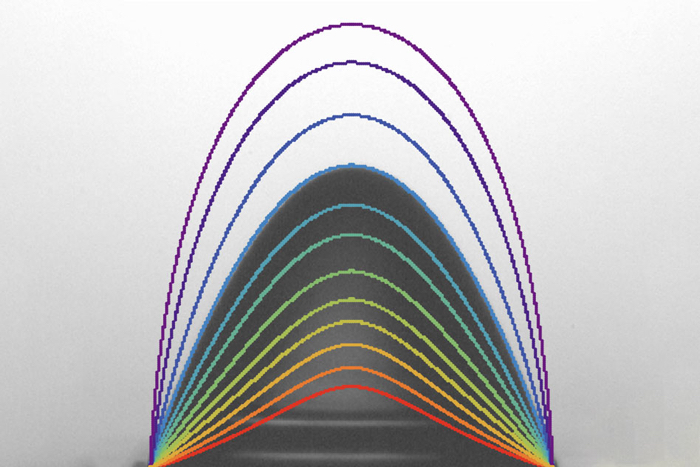Impressions of different water droplet shapes due to varying electric field strength. (MIT)
"At some point, if the electric field is strong enough, the droplet can't find a shape that balances the electrical force," Beroz says, "and at that point, it becomes unstable and bursts."
Now, it looks like we've finally figured it out.
In experiments, Beroz and his team observed the behaviour of water droplets dispensed onto an electrified metal plate, filming the results with a high-speed camera.
By focusing on the exact moment before the electric field forced the droplet to burst – and observing its critical stable shape in that instant – the researchers discovered the stability limit is governed by a power law that can explain the burst threshold of droplets on a surface (whether stationary or sliding) or free-floating in the air.
According to the researchers, the power law formula they found primarily revolves around the droplet's volume and radius – whereas previous theoretical approaches had looked to droplet height (and radius) to calculate the stability limit.
"For the last 100 years, the convention was to choose height," Beroz says.
"But as a droplet deforms, its height changes, and therefore the mathematical complexity of the problem is inherent in the height. On the other hand, a droplet's volume remains fixed regardless of how it deforms in the electric field."
With the new equation, the team says that as long as you know four of five necessary parameters – droplet surface tension, electric field strength, and air electric permittivity, in addition to volume and radius – you can always calculate the fifth parameter, and therefore figure out the stability limit.
It's an achievement that's been a long time coming, and one that could overhaul our theoretical understanding in several areas of science, leading to potential advancements in industrial processes such as electrospinning, electrostatic filtration, and demulsification.
"From a theoretical point of view, it was an unexpectedly simple result given the mathematical complexity of the problem," Beroz says.
The findings are reported in Physical Review Letters.