The 17th-century astronomer Johannes Kepler was one of the first to muse about the structure of snowflakes. Why are they so symmetrical? How does one side know how long the opposite side has grown?
Kepler thought it was all down to what we would now call a "morphogenic field" – that things want to have the form they have. Science has since discounted this idea.
But the question of why snowflakes and similar structures are so symmetrical is nevertheless not entirely understood.
Modern science shows just how fundamental the question is: look at all the spiral galaxies out there. They can be half a million light years across, but they still preserve their symmetry. How? In our new study, published in Scientific Reports, we present an explanation.
We have shown that information and "entropy" – a measure of the disorder of a system – are linked together ("info-entropy") in a way exactly analogous to electric and magnetic fields ("electromagnetism").
Electric currents produce magnetic fields, while changing magnetic fields produce electric currents. Information and entropy influence each other in the same way.
Entropy is a fundamental concept in physics. For example, because entropy can never decrease (disorder always increases) you can turn an egg into scrambled eggs but not the other way around. If you move information around you must also increase entropy – a phone call has an entropy cost.
We showed that entropy and information can be treated as a field and that they are related to geometry. Think of the two strands of the DNA double helix winding around each other.
Light waves have the same structure, where the two strands are the electric and magnetic fields. We showed mathematically that the relationship between information and entropy can be visualised using just the same geometry.
We wanted to see if our theory could predict things in the real world, and decided to try and calculate how much energy you'd need to convert one form of DNA to another. DNA is after all a spiral and a form of information.
This was actually done in extraordinarily precise measurements some 16 years ago. The researchers pulled a DNA molecule straight (DNA likes to curl up), and twisted it 4,800 turns while holding the ends with optical tweezers.
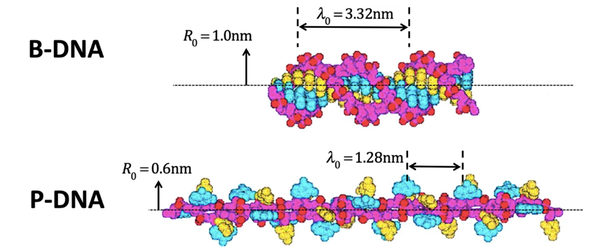Two forms of DNA. (Parker & Jeynes, Scientific Reports, 2019)
The DNA flipped from one form to another, as in the picture above. The researchers could then calculate the energy difference between the two forms.
But our theory could calculate this energy difference, too. We knew the entropy of each of the two versions of this DNA molecule, and the energy is simply the product of entropy and temperature. Our result was spot on – the theory seemed to hold up.
From tiny to enormous
Spiral galaxies are double spirals just as DNA is a double helix – mathematically speaking they have similar geometries.
Our theory shows directly why the two arms of the spiral galaxies are symmetrical – it's because info-entropy fields give rise to forces (like other fields). The stars in the galaxy are simply choreographed by an entropic force to line up into a pair of such spirals to maximise entropy.
But we wanted to get some real numbers, too. We therefore decided to try to calculate the mass of our galaxy from our theory. We know how heavy the Milky Way appears to be from how fast the stars move near the galactic edge – it is about 1.3 trillion Sun masses.
Strangely, this is actually much more than the mass of all the visible stars in the galaxy. To be able to explain this discrepancy and account for why stars move so much faster than expected, astronomers came up with the idea of "dark matter" – unseen mass lurking in the galaxy, increasing its gravitational pull on the stars.
We needed to know the entropy of the galaxy for our calculations. Luckily, the mathematical physicist Roger Penrose showed that this entropy is dominated by the entropy of its central super-massive black hole.
We know the mass of this black hole (4.3 million Sun masses). And amazingly, when you know the mass of a black hole, there is an equation, discovered by the late physicist Stephen Hawking, that calculates its entropy. Hawking also discovered how to calculate the "temperature" at its surface, or "event horizon".
If you can assign a "temperature" to the black hole event horizon – which has no stuff in it to have temperature – why not also assign a temperature to a galaxy? We argue in our paper that this is reasonable (using what's known as the "holographic principle").
So we used our info-entropy equations to calculate the galaxy's holographic temperature.
Then it gets easy. We know that the galactic energy is given by the product of its entropy and temperature. And when we know the energy we can find out the mass thanks to Einstein's famous equation: E=mc2.
This time the result was not exactly spot on, but it was reasonably close given our highly simplified model of the galaxy. The info-entropic geometry of a galaxy not only explains how entropic forces create the beautifully symmetric shape and keep it, but also accounts for all the mass that appears to be evident in it.
This means that we don't actually need dark matter after all. According to our model, the galactic entropy gives rise to such a large quantity of additional energy that it modifies the observed dynamics of the galaxy – making stars at the edge move faster than expected.
This is exactly what dark matter was meant to explain. The energy isn't directly observable as mass, but its presence is certainly supported by the astronomical observations – explaining why dark matter searches have so far found nothing.
There is a lot of research supporting the idea of dark matter though. Our theory suggests an alternative explanation of the observations, and needs no new physics. Of course, more detailed work is needed to verify that the true complexity of the observations can also be modelled successfully.
We think that the "morphogenic field" Kepler was seeking really does exist, and is actually the effect of the intertwining of information and entropy. After four long centuries, it seems Kepler has finally been vindicated.
Chris Jeynes, Senior researcher, University of Surrey and Michael Parker, Visiting Fellow, University of Essex.
This article is republished from The Conversation under a Creative Commons license. Read the original article.