While maths might seem like a purely formulaic pursuit, the patterns and ratios it produces can help create some of history's most striking works of art - as anyone who's read The Da Vinci Code will know.
Just take a look at Leonardo Da Vinci's geometric sketches inside Luca Pacioli's book, De Divina Proportione (The Divine Proportion), or M. C. Escher's mathematically accurate prints, and you'll realise that the purity and patterns found within numbers and forumulae can transform the world into a more beautiful place.
But it's not just historically - even today, mathematicians and artists are bringing their skills together to create some truly beautiful works. And with the help of computers, they've taken things to a whole new level.
Below are seven of our favourite recent adventures in maths and art.
1. Simon Beck's snow art
Simon Beck is a mapmaker by trade, but his passion for art inspired him to create these epic 'snowscapes' in the European Alps.
Each one takes 11 hours and Beck makes them using nothing but a compass and his snowshoes, and most of them depict mathematical formation such as a Koch snowflake or a Sierpinski triangle, which you can see below.
He chooses to draw with maths because of the simplicity of the patterns, he told Alex Bellos over at The Guardian in 2014. "You can get to drawing much sooner," he says. "You are just following simple rules. You don't have to keep referring to a diagram. You can do it from memory. And they just look the best."
See more here.
 Simon Beck
Simon Beck
 Simon Beck
Simon Beck
2. Hamid Naderi Yeganeh's computer illustrations
Iranian arist Hamid Naderi Yeganeh uses mathematical formulae to create intricate, computer-generated illustations - his program can create thousands a day. The emerging shapes were always beautiful, but he began to realise that some of them also randomly represented real-life objects.
"I change the formulae to find better shapes. But I don't know anything about the results of the programs before running them. For example, I found [the] boat and animals accidentally," he told Science Friday.
He now tweaks his data to make more of these recognisable shakes, in order to help share "the power of mathematics" with the world. He's also made his formulae and illustrations open to the public on his website so anyone can create their own.
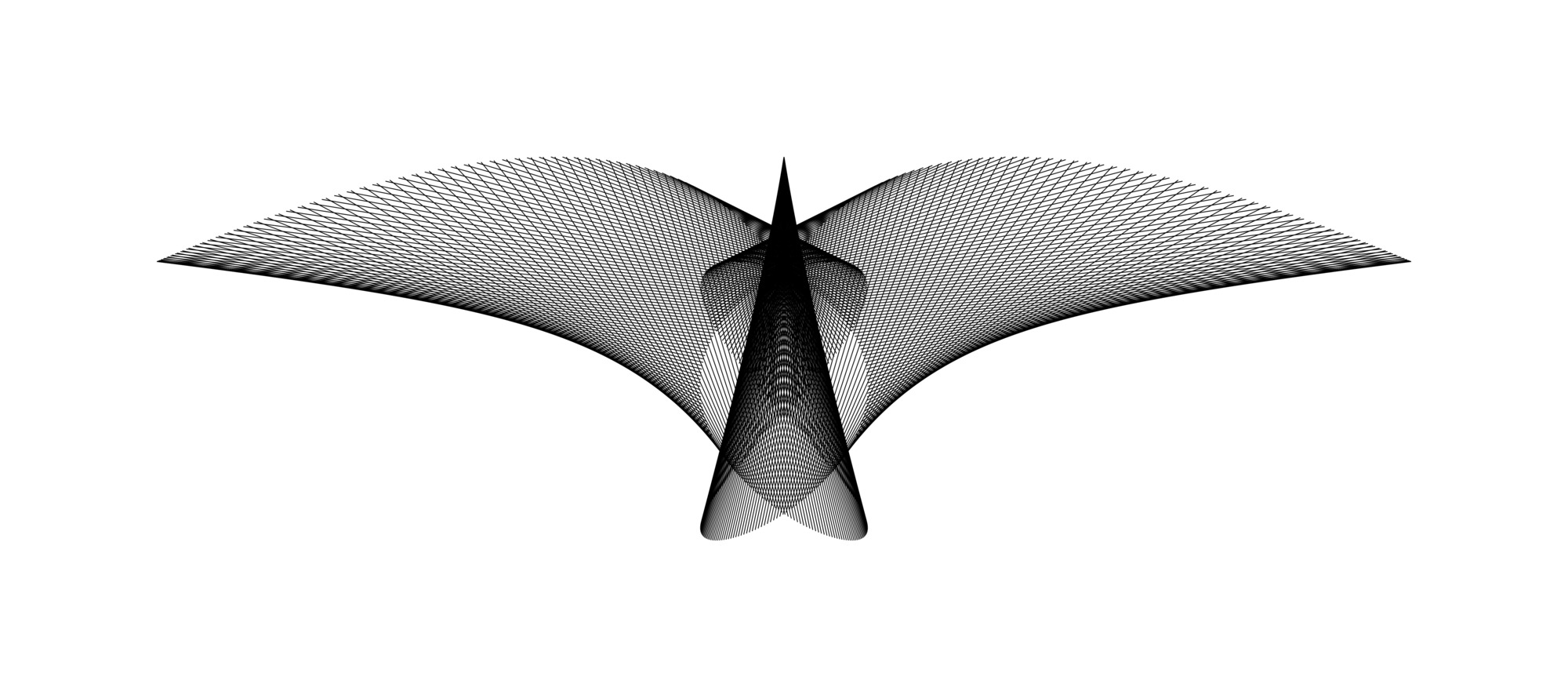 Hamid Naderi Yeganeh
Hamid Naderi Yeganeh
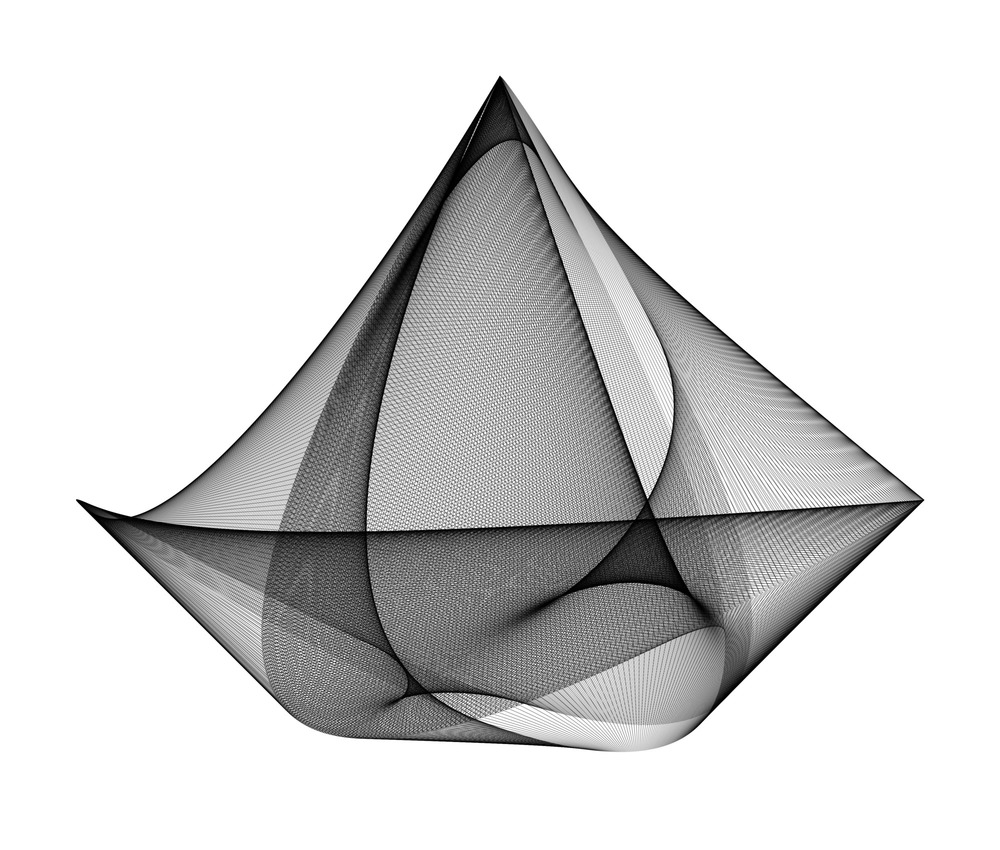 Hamid Naderi Yeganeh
Hamid Naderi Yeganeh
3. Tom Beddard's Fabergé Fractals
Fractals are patterns that repeat at every scale - creating never-ending swirls, lines, and curves that have been loved in the natural, math, and art worlds for centuries. To show his appreciation, UK physicist Tom Beddard decided to create digital renderings of 3D Fabergé eggs covered in these detailed fractal patterns.
"The 3D fractals are generated by iterative formulae whereby the output of one iteration forms the input for the next," Beddard told My Modern Met. "The formulae effectively fold, scale, rotate or flip space. They are truly fractal in the fact that more and more detail can be revealed the closer to the surface you travel."
Either way, they're incredibly beautiful. See more of his work here.
 Tom Beddard
Tom Beddard
 Tom Beddard
Tom Beddard
4. Liz Blakenship and Daniel Ashlock's taxonomy of fractals
Even if you're a die-hard fractals fan, what you might not know is that there are many different types of fractals out there, and they don't all look like the ones above. That's why Liz Blakenship and Daniel Ashlock have created a taxonomy of fractals, complete with illustrations to show them off in all their glory.
These L-system fractals, for example, look more like exotic ferns than mathematical diagrams. But they're still made up of repeating patterns. "These L-systems use two angles, given by the letters A and B and two distances given by the letters C and D," Ashlock and Blakenship write.
See more fractals in their taxonomy.
 Liz Blakenship and Daniel Ashlock
Liz Blakenship and Daniel Ashlock
 Liz Blakenship and Daniel Ashlock
Liz Blakenship and Daniel Ashlock
5. Henry Segerman's 3D models
Australian mathematician Henry Segerman creates illustrations and 3D printed models that express mathematical formulae and concepts, to help his students better understand them.
"Students should be given time to understand the language of mathematics and to creatively apply it to solve problems. Often, maths classes never go beyond rote exercises, in contrast with an English class in which we would use the language to create a new idea, a story or poem," Segerman says.
"The language of mathematics is often less accessible than the language of art, but I can try to translate from one to the other, producing a picture or sculpture that expresses a mathematical idea."
 Henry Segerman
Henry Segerman
6. The Hevea Project's models of isometric embedding
Isometric embedding is a little complex to understand, but it was fundamental work done by A Beautiful Mind mathematician John Nash, along with Nicolaas Kuiper - and it explains how the entire world can be contained in grain of sand.
"This sounds ridiculous. For instance, take a sphere - say the surface of a tennis ball - and imagine shrinking it down to have a nanometre radius," writes Daniel Matthews about isometric embedding. "Nash and Kuiper show that by 'ruffling' the surface sufficiently (but always smoothly; no creasing or folding or ripping or tearing allowed!) you can have an isometric copy of your original tennis ball, all contained within this nanometre radius."
A French team of mathematicians calling themselves the Hevea Project have now created digital constructions of what this would look like, and the results are spectacular.
Read more about their work here.
 Hevea Project
Hevea Project
 Hevea Project
Hevea Project
7. Kerry Mitchell's celebration of the Curiosity landing on Mars
If there's one thing better than mathematical art, it's mathematical art that celebrates space exploration, like this image created by renowned artist and former NASA engineer, Kerry Mitchell, in 2012 to celebrate the Curiosity rover landing on Mars.
Although it looks like a regular painting, Mitchell creates all his art using algorithms and fractals.
"This image is in my Mandelbrot and Julia sets collection of images showing the dynamics of a formula under repeated iteration. 'Curiosity' celebrates both the unsung measure of central tendency, the harmonic mean, and the Curiosity rover's landing on Mars in August 2012," writes Mitchell.
See more.
 Kerry Mitchell
Kerry Mitchell
H/T: The Science Explorer
