Leonardo da Vinci, the famous Italian polymath who painted the Mona Lisa, had a sophisticated geometric understanding way ahead of his time.
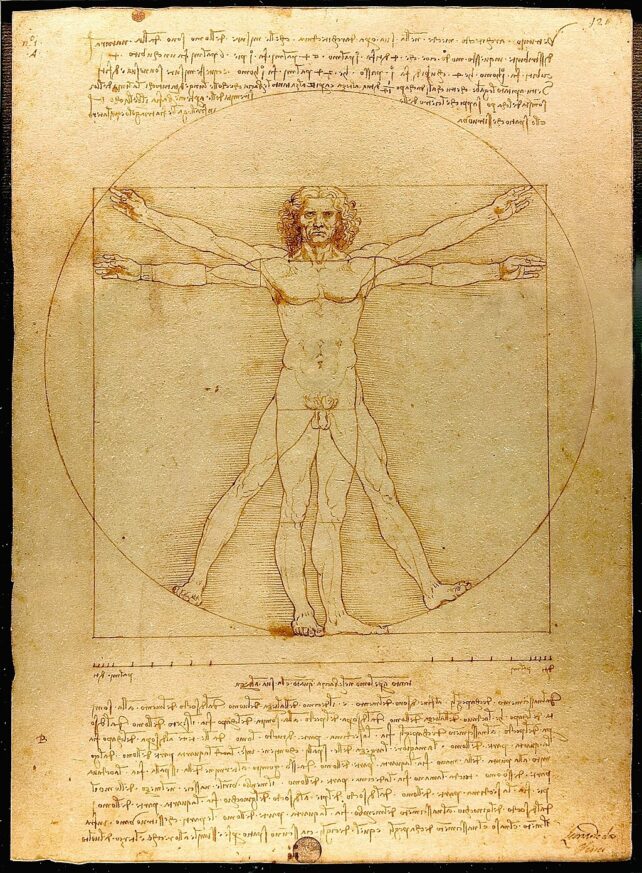
To draw the Vitruvian Man in 1490 – an illustration of the 'ideal' human body – the Renaissance man may have relied on a mathematical ratio not formally established until the 19th century.
It's one of the most iconic images of all time, and yet for more than 500 years, no one could figure out why da Vinci chose such specific proportions for the arms and legs.
A London dentist thinks he's solved the mystery at last.
Related: Four Ways Leonardo Da Vinci Was Well Ahead of His Time
Rory Mac Sweeney has found a crucial hidden detail, tucked in the Vitruvian Man's crotch: an equilateral triangle that he thinks may explain "one of the most analyzed yet cryptic works in art history."
The Vitruvian Man is partly inspired by the writings of Roman architect Vitruvius, who argued that the perfect human body should fit inside a circle and square.
Da Vinci's drawing uses a square to precisely contain a 'cruciform pose', with arms outstretched and legs in. The circle, meanwhile, encompasses a posture where the arms are raised and the legs are spread.
A popular explanation is that da Vinci chose the Vitruvian Man's proportions based on the Golden Ratio Theory, but the measurements don't quite match up.
According to Mac Sweeney, "the solution to this geometric mystery has been hiding in plain sight".
"If you open your legs… and raise your hands enough that your extended fingers touch the line of the top of your head… the space between the legs will be an equilateral triangle," da Vinci wrote in his notes for the Vitruvian Man.
When Mac Sweeney did the math on this triangle, he found that the spread of the man's feet and the height of his navel created a ratio of around 1.64 to 1.65.
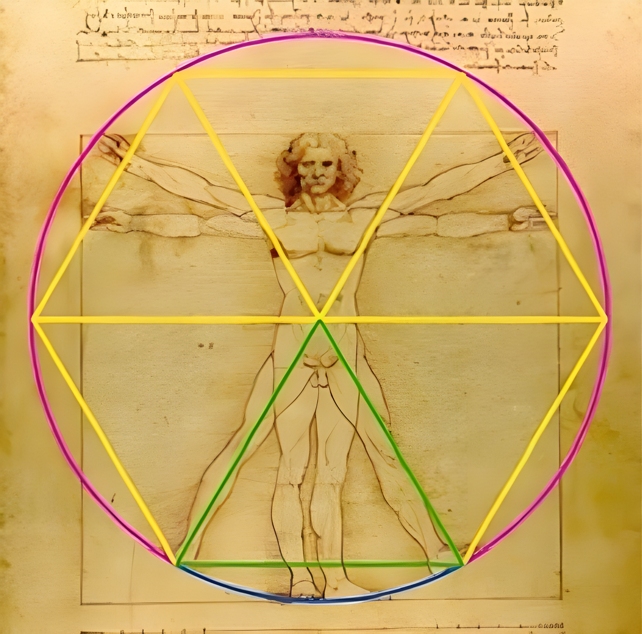
That's very close to the tetrahedral ratio of 1.633 – a uniquely balanced geometric form, officially established in 1917.
The ratio is used to establish the optimum way to pack spheres. If four spheres are connected as closely as possible into a pyramid shape, for instance, then the height to base ratio from their centers will be 1.633.
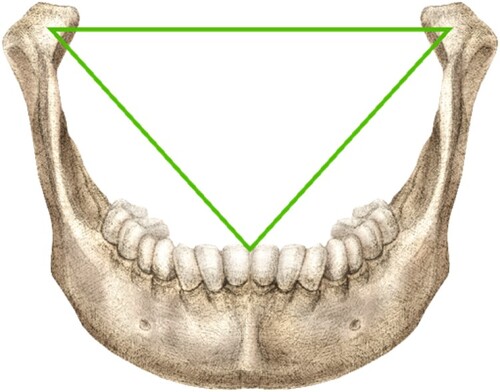
Perhaps Mac Sweeney recognized the significance of that number because of a similar triangular principle used in dentistry.
Imagined on the human jaw, Bonwill's triangle dictates the optimal positioning for jaw function, used since 1864. Its ratio is also 1.633.
Mac Sweeney doesn't think that's a coincidence.
Similar to minerals, crystals, and other biological packing systems found in nature, Mac Sweeney thinks the human jaw naturally organizes around tetrahedral geometries, which maximize mechanical efficiency.
If the tetrahedral ratio is repeated around our bodies, Mac Sweeney thinks that is because "human anatomy has evolved according to geometric principles that govern optimal spatial organization throughout the universe."
If Mac Sweeney is right, Da Vinci may have stumbled across a universal principle while drawing the Vitruvian Man.
"The same geometric relationships that appear in optimal crystal structures, biological architectures, and Fuller's coordinate systems seem to be encoded in human proportions," writes Mac Sweeney, "suggesting that Leonardo intuited fundamental truths about the mathematical nature of reality itself."
Whether other scientists agree with Mac Sweeney remains to be seen, but the fact that da Vinci mentioned the equilateral triangle in his notes suggests that what lies between the Vitruvian man's legs is important.
The study was published in the Journal of Mathematics and the Arts.
