A gelatinous, single-celled life form has just solved an increasingly complex problem that many researchers use to test algorithms.
Even more impressive is the fact that, as the problem got harder, the slime mould amoeba actually solved the problem in a totally different – and arguably more efficient – way than most algorithms.
The result suggests that these simple lifeforms might actually offer an alternative processing method to conventional computers.
Or, to put it more simply, our state-of-the-art electronic devices could actually learn something from an amoeba. Ouch.
To be clear, the amoeba wasn't faster than computers, not by a long stretch (check out how slow they move in the video below).
But while the problem got exponentially more complex, the amoeba's processing time only increased linearly. You can see why that's a big difference below:
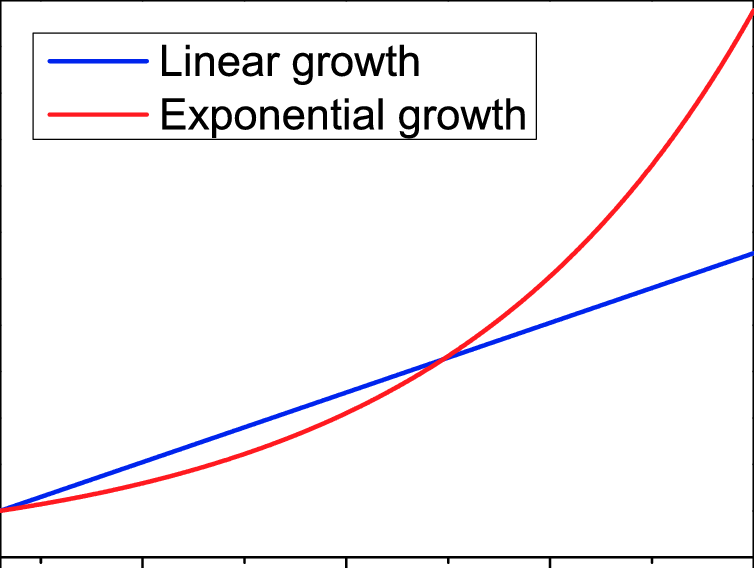Unrelated linear vs exponential graph (Luo, Researchgate)
The problem it had to solve was the Traveling Salesman Problem, or TPS for short. This is basically an optimisation problem which requires a computer to look at a list of cities and figure out the shortest route, so that each city is visited exactly once.
As more cities are added to the itinerary, the problem gets increasingly more complex - with four cities on the list there are only three possible routes to choose between. But for eight cities, the situation jumps up to 2,520 routes.
In other words, it gets exponentially harder - and would take most systems a whole lot more time to figure out the best route.
But a team of researchers from Keio University in Japan decided to give the problem to a "true slime mould" amoeba Physarum polycephalum, and were surprised to find that as the cities increased from four to eight, the single-celled organism only needed a linear amount of more time to figure out a reasonable (almost optimal) route.
"In this study, we show that the time taken by plasmodium to find a reasonably high-quality TSP solution grows linearly as the problem size increases from four to eight," the researchers write in Royal Society Open Science.
"These results may lead to the development of novel analogue computers enabling approximate solutions of complex optimisation problems in linear time."
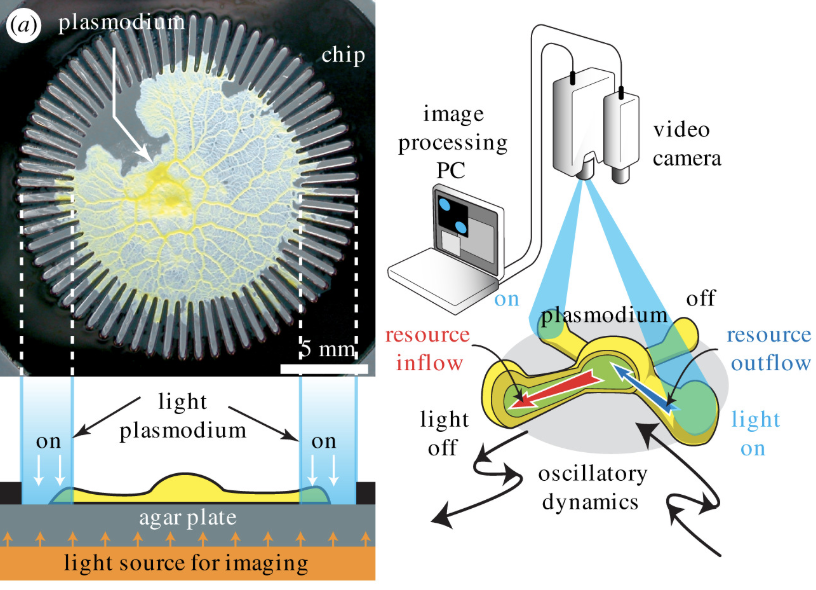
Of course, amoebas don't know what cities are (as far as we know) so in this version of the TSP, the 'cities' were 64 narrow channels (eight 'cities' each containing eight channels) in a round plate placed on top of agar.
To get access to the agar and efficiently absorb nutrients, the amoeba enters the channels.
The salesman 'route' it picks is its constantly changing body shape. So it makes one body shape when it enters one channel, a different body shape when it then enters a second channel, and so on.
(Aono et al. Royal Society Open Science)
To make sure the amoeba entered the 'cities' in an optimal way, the researchers used light (which the amoeba doesn't like) to illuminate certain channels that were too far apart or that it had already visited, and to stop it from entering several channels simultaneously.
To the team's astonishment, it didn't take exponentially longer for the amoeba to figure out a reasonable (nearly optimal) way to enter eight different channels than it did to enter four, despite the increase in the number of possible configurations.
"Interestingly," the team added, "the quality of the solution does not degrade despite the explosive expansion of the search space."
To be fair, conventional computers are pretty slick, and they can also solve the problem in linear time as it gets exponentially harder.
But they actually do it in a completely different way - the amoeba was constantly testing new body shapes at a constant rate and processed optical feedback at the same time, which is something computers could learn from.
The researchers say that they only limited the experiment to eight channels because they couldn't make a plate big enough to test more - but if they could, they think the amoeba's natural urge to seek out a stable equilibrium would see it calculate optimal routes across hundreds of 'cities'.
They've even developed a computer simulation called AmoebaTSP that mimics some of the amoeba's processing patterns - but we still have a lot to learn.
"The mechanism by which the amoeba maintains the quality of the approximate solution, that is, the short route length, remains a mystery," team leader Masashi Aono told Lisa Zyga over at Phys.org.
The Keio team isn't the only one excited by the potential.
In their paper, Aono and team cite research groups suggesting that amoeba-inspired electrical circuits could help tackle classic conundrums such as the constraint satisfaction problem, Boolean satisfiability problem, and even help find walking manoeuvres for multi-legged robots.
That'll do slime mould, that'll do.
The research has been published in Royal Society Open Science.