This article was written by Jason Cole from the Imperial College London, and was originally published at The Conversation.
Electromagnetic radiation - it might sound like something that you'd be better off avoiding, but electromagnetic waves of various kinds underpin our senses and how we interact with the world - from the light emissions through which your eyes perceive these words, to the microwaves that carry the Wi-Fi signal to your laptop or phone on which you're reading it.
More or less every form of modern communication is carried by electromagnetic waves. They whisk through the antenna on your car, travel through walls whenever you need to make a phone call inside, yet also inexplicably reflect from seemingly nothing in the Earth's upper atmosphere.
This happens because the atmosphere becomes a plasma at high altitudes - a state of matter where atoms split apart and electrons are no longer bound to their parent nuclei. Plasmas have interesting properties, as they react very strongly to electromagnetic fields. In this case usefully: at low enough frequencies it becomes possible to bounce radio signals around the world, extending their range.
It's the interesting interactions between high-powered electromagnetic waves and plasmas that my research group and I study. The most intense electromagnetic waves in the world are found in the form of high-power laser pulses. The UK hosts some of the most powerful laser systems in rural Oxfordshire, and the same idea of using electromagnetic waves to accelerate particles is used at the Large Hadron Collider in CERN.
It's all in the maths
We can accurately predict the interactions of intense electromagnetic waves and plasmas, as the underlying physical processes are governed by Maxwell's equations – one of the triumphs of 19th century physics that united electric and magnetic fields and demonstrated that light is a form of electromagnetic wave.
Solving Maxwell's equations by hand can be tortuous, but it transpires that a clever algorithm invented in the 1960s and rediscovered since makes the exercise relatively simple given a sufficiently powerful computer.
Armed with the knowledge of Maxwell's equations and how to solve them, I recently turned my attention to a much simpler but more widespread problem, that of how to simulate and therefore improve the Wi-Fi reception in my flat. While "sufficiently powerful" in an academic sense often means supercomputers with tens of thousands of processors running in parallel, in this case, the sufficiently powerful computer required to run the program turned out to be a smartphone.

For this trick, you will need one Maxwell
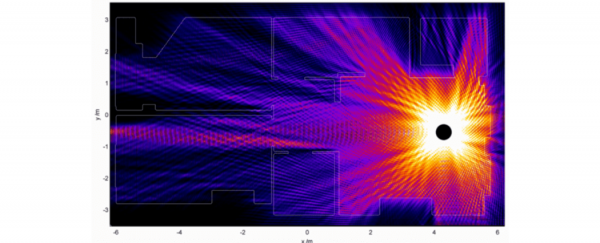
The electromagnetic radiation emanating from the antenna in your wireless router is caused by a small current oscillating at 2.4GHz (2.4 billion times per second). In my model I introduced a current like this and allowed it to oscillate, and Maxwell's equations dictated how the resulting electromagnetic waves flow. By mapping in the actual locations of the walls in my flat, I was able to produce a map of the Wi-Fi signal strength which varied as I moved the virtual router.
The first lesson is clear, if obvious: Wi-Fi signals travels much more easily through free space than walls, so the ideal router position has line-of-sight to where you'll be using it.
Sometimes it appears that the waves have stopped changing, and instead flicker in the same places. This is the phenomenon of a standing wave, where Wi-Fi reflections overlap and cancel each other out. These dark spots on the map (or "not spots") indicate a low Wi-Fi signal, and are separated by several centimetres. Recently, a fellow enthusiast managed to map this phenomenon in three dimensions, as explained in this video.
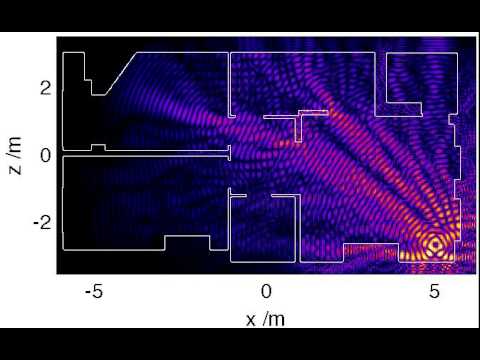
So the second lesson is less obvious and more interesting: if reception is poor in a particular position, even a slight change of the router's position may produce significant improvement in signal strength, as any signal dark spots will also move.
101 uses for electromagnetic waves
After publishing my findings I was struck by the number of people eager to perform simulations of their own. Ever eager to spread the gospel of electromagnetism, I bundled the simulation into an Android app to provide others with a simulated electromagnetic wave-based solution to a common modern problem: where's the best place for my Wi-Fi router?
Assuming few would be interested, I was surprised when news spread via social media and the several thousand copies of the app sold over the course of a few hours.
Sales have gradually dwindled but the message remains clear: not only are electromagnetic waves fascinating, mathematically elegant and supremely useful, they can make your life easier, your Internet connection stronger, and even make you a bit of money too.
This article was originally published at The Conversation. Read the original article.