What began as a bonus question in a high school math contest has resulted in a staggering 10 new ways to prove the ancient mathematical rule of Pythagoras' theorem.
It's long been claimed impossible to use trigonometry to prove what is effectively a theorem that's fundamental to trigonometry. This falls into the logical fallacy of circular thinking by trying to prove an idea with the idea itself.
"There are no trigonometric proofs because all the fundamental formulae of trigonometry are themselves based upon the truth of the Pythagorean theorem," mathematician Elisha Loomis had written in 1927.
But two US high school classmates, Ne'Kiya Jackson and Calcea Johnson, achieved the 'impossible' during their final year of high school in 2023.
Now they've published those results along with a further nine proofs.
"There were many times when both of us wanted to abandon this project, but we decided to persevere to finish what we started," Jackson and Johnson write in their paper.

Pythagoras' theorem describes the relationship between the three sides of a right-angled triangle.
It is incredibly useful for engineering and construction and was used by humans centuries before the equation was attributed to Pythagoras, including, some contend, in the building of Stonehenge.
The theorem is a fundamental law in the field of trigonometry, which essentially deals with the relationships between sides and angles of triangles. You likely recall having the equation a2+b2=c2 drilled into you at school.
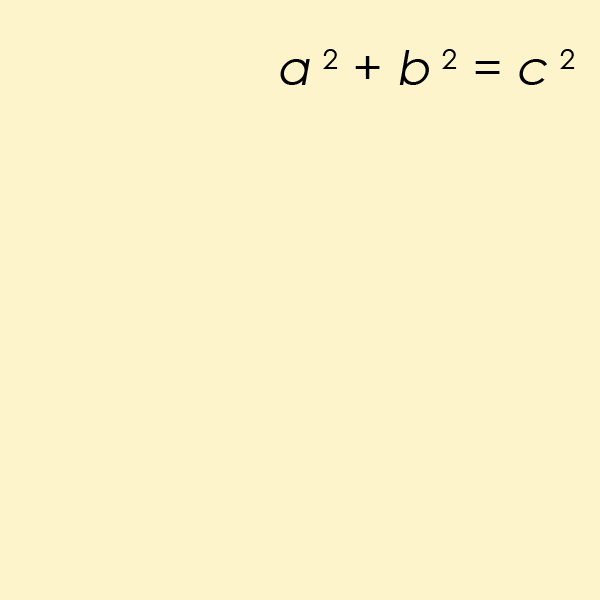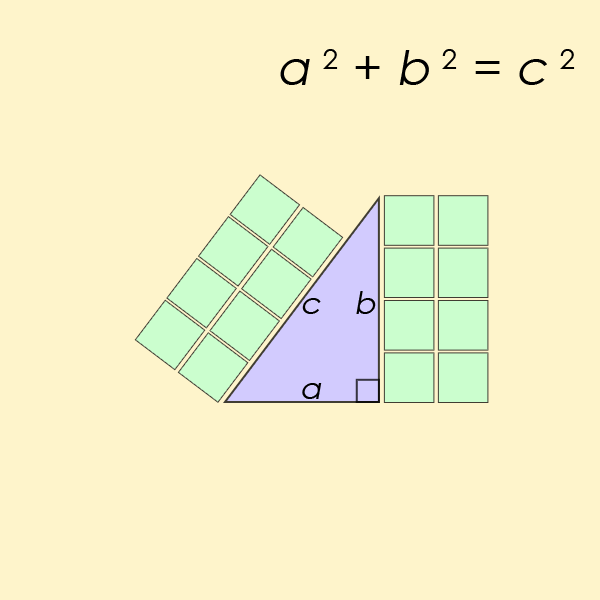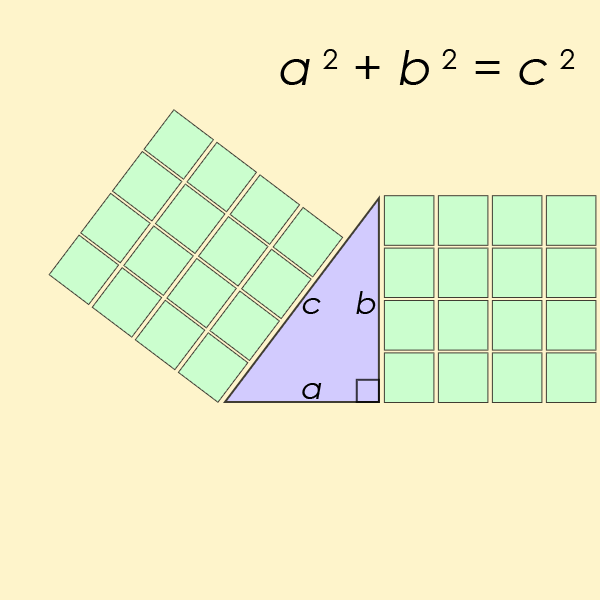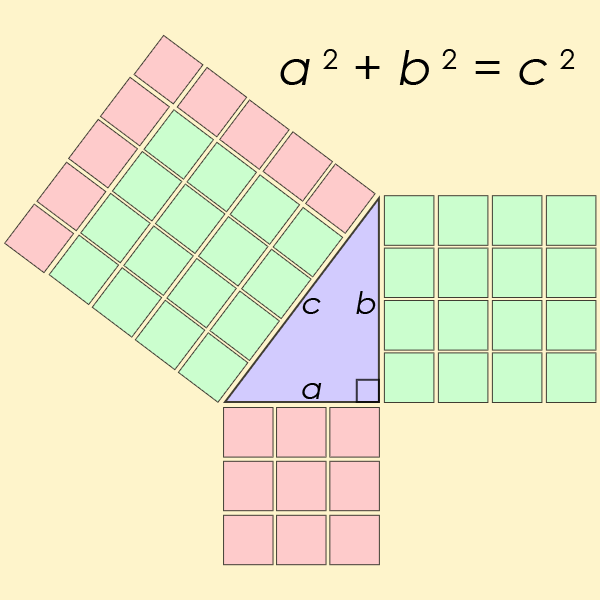
"Students may not realize that two competing versions of trigonometry have been stamped onto the same terminology," explain Jackson and Johnson.
"In that case, trying to make sense of trigonometry can be like trying to make sense of a picture where two different images have been printed on top of each other."
By disentangling these two related but different variations, Jackson and Johnson were able to come up with novel solutions using the Law of Sines, sidestepping direct circular thinking.
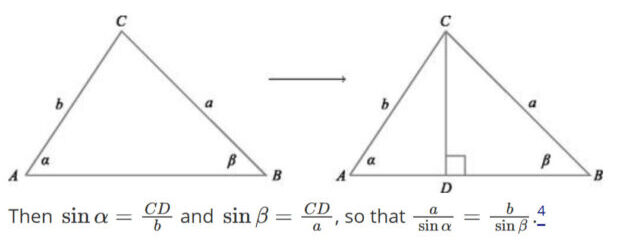
Jackson and Johnson outline this method in their new paper, although they note the line between trigonometric and non trigonometric is somewhat subjective.
They also point out that under their definition, two other experienced mathematicians, J. Zimba and N. Luzia, have proven the theorem using trigonometry too, defying past assertions that this was impossible.
In one of their proofs, the two students took the definition of calculating with triangles to its extreme by filling one larger triangle with sequences of smaller triangles and using calculus to find the measurements of the original triangle's sides.
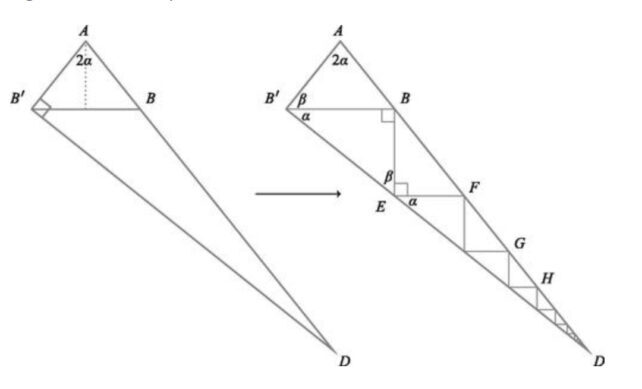
"It looks like nothing I've ever seen," University of Connecticut mathematician Álvaro Lozano-Robledo told Nikk Ogasa at Science News.
Altogether, Jackson and Johnson provide one proof for right triangles that have two equal sides and another four proofs for right triangles with unequal sides, leaving at least five more for "the interested reader to discover."
"To have a paper published at such a young age – it's really mind-blowing," says Johnson, who is now studying environmental engineering. Jackson is now studying pharmacy.
"Their results call attention to the promise of the fresh perspective of students on the field," says Della Dumbaugh, editor-in-chief of the journal they are published in.
This research was published in the American Mathematical Monthly.
