Physicists are one step closer to nutting out a complete mathematical theory for predicting how blood and other peculiar fluids flow. These bizarre behaviors have puzzled researchers for decades.
Not that we've tried, but blood actually deforms slightly when nudged, and strangely, it thickens up when a strong, sudden force is applied – shifting from a thin, watery substance to a more viscous, almost solid one.
Another (more hygienic) example of this is the classic trick you might remember from school science demonstrations: cornstarch mixed with water. If you stir it slowly, nothing appears untoward, but squeeze a handful of the mixture, and it solidifies into a rubbery ball. Open your hand, and it'll drip like liquid again.
What's actually happening is an example of a non-Newtonian fluid, a type of fluid that disobeys Newton's law of viscosity and is instead characterized by its odd relationship between stress, the forces applied to the liquid, and strain, how it deforms in response.
But that's not the only weird thing about non-Newtonian fluids. They also display a particularly chaotic fluid motion called elastic turbulence that exists only in these fluids, not obedient Newtonian ones.
Turbulence, of any kind, turns an otherwise orderly laminar flow into a chaotic, churning mess that in industrial settings, makes mixing or pumping fluids difficult – or a boat ride on a fast-flowing river bumpy.
It usually happens at high flow speeds, and although it may be a familiar phenomenon, describing turbulence in its various forms "remains one of the last unsolved problems in classical physics," proclaim the researchers behind this new study of elastic turbulence.
Researchers realized in the 1990s that in watery solutions containing polymers – which are long, repeating chains of molecules – the elasticity of the polymers stretching and contracting caused laminar flows to become unstable.
At the start of the 21st century, they discovered elastic turbulence, which is even more dramatic, emerging in slow laminar flows that are usually smooth.
Elastic turbulence is thought to arise in non-Newtonian fluids, which consist of ultra-fine particles, polymers, or microscopic cells suspended in watery liquids, from the way these particles interact and move. Without particles in the solution, the phenomenon disappears.
Scientists had thought that elastic turbulence was utterly different from the classic turbulence of Newtonian fluids, which behave in a much more predictable manner. But the two phenomena might have more in common than previously thought, according to the team's new modeling.
Led by Marco Rosti, an aeronautical engineer studying fluid dynamics at the Okinawa Institute of Science and Technology in Japan, the team measured the velocity of non-Newtonian fluid flows and calculated the difference at three points, not the usual two used to measure and study classical turbulence.
They discovered that non-Newtonian fluids with elastic turbulence display intermittent fluctuations in velocity at slow flow speeds, like Newtonian fluids do at high flows – a finding that helped them make statistical predictions about how the non-Newtonian fluid behaved.
"Our results show that elastic turbulence has a universal power-law decay of energy and a so far unknown intermittent behavior," explains Rosti. "These findings allow us to look at the problem of elastic turbulence from a new angle."
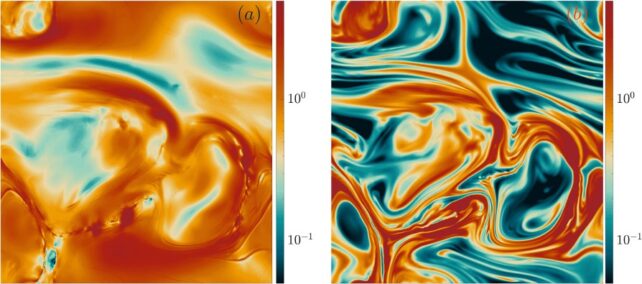
The study adds to other research efforts where physicists have been making strides in describing non-Newtonian fluids, which have puzzled researchers with their strange properties since the 1930s – when they didn't have the instruments or computers to measure and simulate fluid flows like we do today.
In 2019, researchers at Massachusetts Institute of Technology (MIT) developed a 3D model that could describe how ultrafine-particle suspensions, like a cornstarch mixture, turn from a liquid to a solid and back again, under various conditions.
The industrial applications of such a model are quite useful, allowing researchers to predict and optimize the behavior of slurries as they flow between vats in industrial plants, for example.

The new model developed by Rosti's team could have similarly practical uses.
"With a perfect theory" – if such a thing exists – "we could make predictions about the flow and design devices that can alter mixing of liquids," says Rosti. "This might be useful when working with biological solutions," such as donated blood and lymph fluid.
Or, when the rest of us are mucking around with ketchup, custard, and toothpaste – three other fun examples of non-Newtonian fluids.
The study has been published in Nature Communications.
