The word uncertainty is used a lot in quantum mechanics. One school of thought is that this means there's something out there in the world that we are uncertain about. But most physicists believe nature itself is uncertain.
Intrinsic uncertainty was central to the way German physicist Werner Heisenberg, one of the originators of modern quantum mechanics, presented the theory.
He put forward the Uncertainty Principle that showed we can never know all the properties of a particle at the same time.
For example, measuring the particle's position would allow us to know its position. But this measurement would necessarily disturb its velocity, by an amount inversely proportional to the accuracy of the position measurement.
Was Heisenberg wrong?
Heisenberg used the Uncertainty Principle to explain how measurement would destroy that classic feature of quantum mechanics, the two-slit interference pattern (more on this below).
But back in the 1990s, some eminent quantum physicists claimed to have proved it is possible to determine which of the two slits a particle goes through, without significantly disturbing its velocity.
Does that mean Heisenberg's explanation must be wrong? In work just published in Science Advances, my experimental colleagues and I have shown that it would be unwise to jump to that conclusion.
We show a velocity disturbance - of the size expected from the Uncertainty Principle - always exists, in a certain sense.
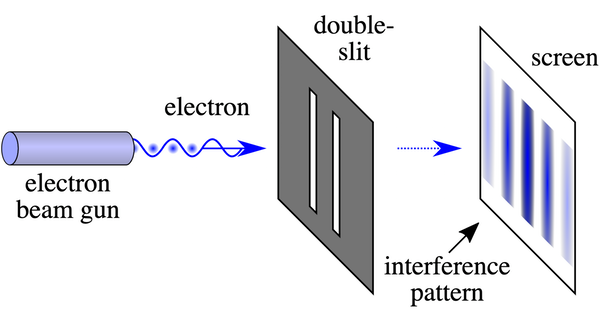
But before getting into the details we need to explain briefly about the two-slit experiment.
The two-slit experiment
In this type of experiment there is a barrier with two holes or slits. We also have a quantum particle with a position uncertainty large enough to cover both slits if it is fired at the barrier.
Since we can't know which slit the particle goes through, it acts as if it goes through both slits.
The signature of this is the so-called "interference pattern": ripples in the distribution of where the particle is likely to be found at a screen in the far field beyond the slits, meaning a long way (often several metres) past the slits.
 (Wikimedia/NekoJaNekoJa/Johannes Kalliauer, CC BY-SA)
(Wikimedia/NekoJaNekoJa/Johannes Kalliauer, CC BY-SA)
But what if we put a measuring device near the barrier to find out which slit the particle goes through? Will we still see the interference pattern?
We know the answer is no, and Heisenberg's explanation was that if the position measurement is accurate enough to tell which slit the particle goes through, it will give a random disturbance to its velocity just large enough to affect where it ends up in the far field, and thus wash out the ripples of interference.
What the eminent quantum physicists realised is that finding out which slit the particle goes through doesn't require a position measurement as such. Any measurement that gives different results depending on which slit the particle goes through will do.
And they came up with a device whose effect on the particle is not that of a random velocity kick as it goes through. Hence, they argued, it is not Heisenberg's Uncertainty Principle that explains the loss of interference, but some other mechanism.
As Heisenberg predicted
We don't have to get into what they claimed was the mechanism for destroying interference, because our experiment has shown there is an effect on the velocity of the particle, of just the size Heisenberg predicted.
We saw what others have missed because this velocity disturbance doesn't happen as the particle goes through the measurement device. Rather it is delayed until the particle is well past the slits, on the way towards the far field.
How is this possible? Well, because quantum particles are not really just particles. They are also waves.
In fact, the theory behind our experiment was one in which both wave and particle nature are manifest - the wave guides the motion of the particle according to the interpretation introduced by theoretical physicist David Bohm, a generation after Heisenberg.
Let's experiment
In our latest experiment, scientists in China followed a technique suggested by me in 2007 to reconstruct the hypothesised motion of the quantum particles, from many different possible starting points across both slits, and for both results of the measurement.
They compared the velocities over time when there was no measurement device present to those when there was, and so determined the change in the velocities as a result of the measurement.
The experiment showed that the effect of the measurement on the velocity of the particles continued long after the particles had cleared the measurement device itself, as far as 5 metres away from it.
By that point, in the far field, the cumulative change in velocity was just large enough, on average, to wash out the ripples in the interference pattern.
So, in the end, Heisenberg's Uncertainty Principle emerges triumphant.
The take-home message? Don't make far-reaching claims about what principle can or cannot explain a phenomenon until you have considered all theoretical formulations of the principle.
Yes, that's a bit of an abstract message, but it's advice that could apply in fields far from physics. ![]()
Howard Wiseman, Director, Centre for Quantum Dynamics, Griffith University.
This article is republished from The Conversation under a Creative Commons license. Read the original article.
