When a spacecraft arrives at its destination, it settles into an orbit for science operations. But after the primary mission is complete, there might be other interesting orbits where scientists would like to explore. Maneuvering to a different orbit requires fuel, limiting a spacecraft's number of maneuvers.
Researchers have discovered that some orbital paths allow for no-fuel orbital changes. But the figuring out these paths also are computationally expensive.
Knot theory has been shown to find these pathways more easily, allowing the most fuel-efficient routes to be plotted. This is similar to how our GPS mapping software plots the most efficient routes for us here on Earth.
In mathematics, knot theory is the study of closed curves in three dimensions. Think of it as looking at a knotted necklace or a tangle of fishing line, and figuring out how to untangle them in the most efficient manner.
In the same way, a spacecraft's path could be computed in a crowded planetary system – around Jupiter and all its moons, for example – where the best, simplest and least tangled route could be computed mathematically.
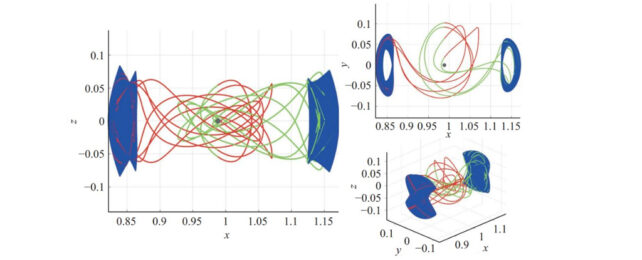
According to a new paper in the journal Astrodynamics, "Applications of knot theory to the detection of heteroclinic connections between quasi-periodic orbits," using knot theory to untangle complicated spacecraft routes would decrease the amount of computer power or just plain guesswork in plotting out changes in spacecraft orbits.
"Previously, when the likes of NASA wanted to plot a route, their calculations relied on either brute force or guesswork," said Danny Owen, a postgraduate research student in astrodynamics, in a press release from the University of Surrey. "Our new technique neatly reveals all possible routes a spacecraft could take from A to B, as long as both orbits share a common energy level."
Owen added that this new process makes the task of planning missions much simpler. "We think of it as a tube [subway] map for space," he said.
Spacecraft navigation is complicated by the fact that nothing in space is a fixed position. Navigators must meet the challenges of calculating the exact speeds and orientations of a rotating Earth, a rotating target destination, as well as a moving spacecraft, while all are simultaneously traveling in their own orbits around the Sun.
Since fuel is a limited resource for most missions, it would be beneficial to require the least amount of fuel possible in making any changes to the course of a spacecraft in orbit.
Spacecraft navigators use something called heteroclinic orbits – often called heteroclinic connections – which are paths that allow a spacecraft to travel from one orbit to another using the most efficient amount of fuel, or sometimes no fuel at all. But this usually takes a large amount of computer power or a lot of time to figure out.
But Owen and co-author Nicola Baresi, a lecturer in Orbital Mechanics at the University of Surrey, wrote that by using knot theory, they have developed "a method of robustly detecting heteroclinic connections," they wrote in their paper, to quickly generate rough trajectories – which can then be refined. This gives spacecraft navigators a full list of all possible routes from a designated orbit, and the one that best fits the mission can be chosen. They can then choose the one that best suits their mission.
The researchers tested their technique on various planetary systems, including the Moon, and the Galilean moons of Jupiter.
"Spurred on by NASA's Artemis program, the new Moon race is inspiring mission designers around the world to research fuel-efficient routes that can better and more efficiently explore the vicinity of the Moon," said Baresi.
"Not only does our technique make that cumbersome task more straightforward, but it can also be applied to other planetary systems, such as the icy moons of Saturn and Jupiter."
This article was originally published by Universe Today. Read the original article.