Mountains are some of the mightiest geographic features on our planet, and no two ranges are the same. Some have soaring peaks, ragged ridges, and deep ravines, while others gently roll away in wavy hills and wide valleys.
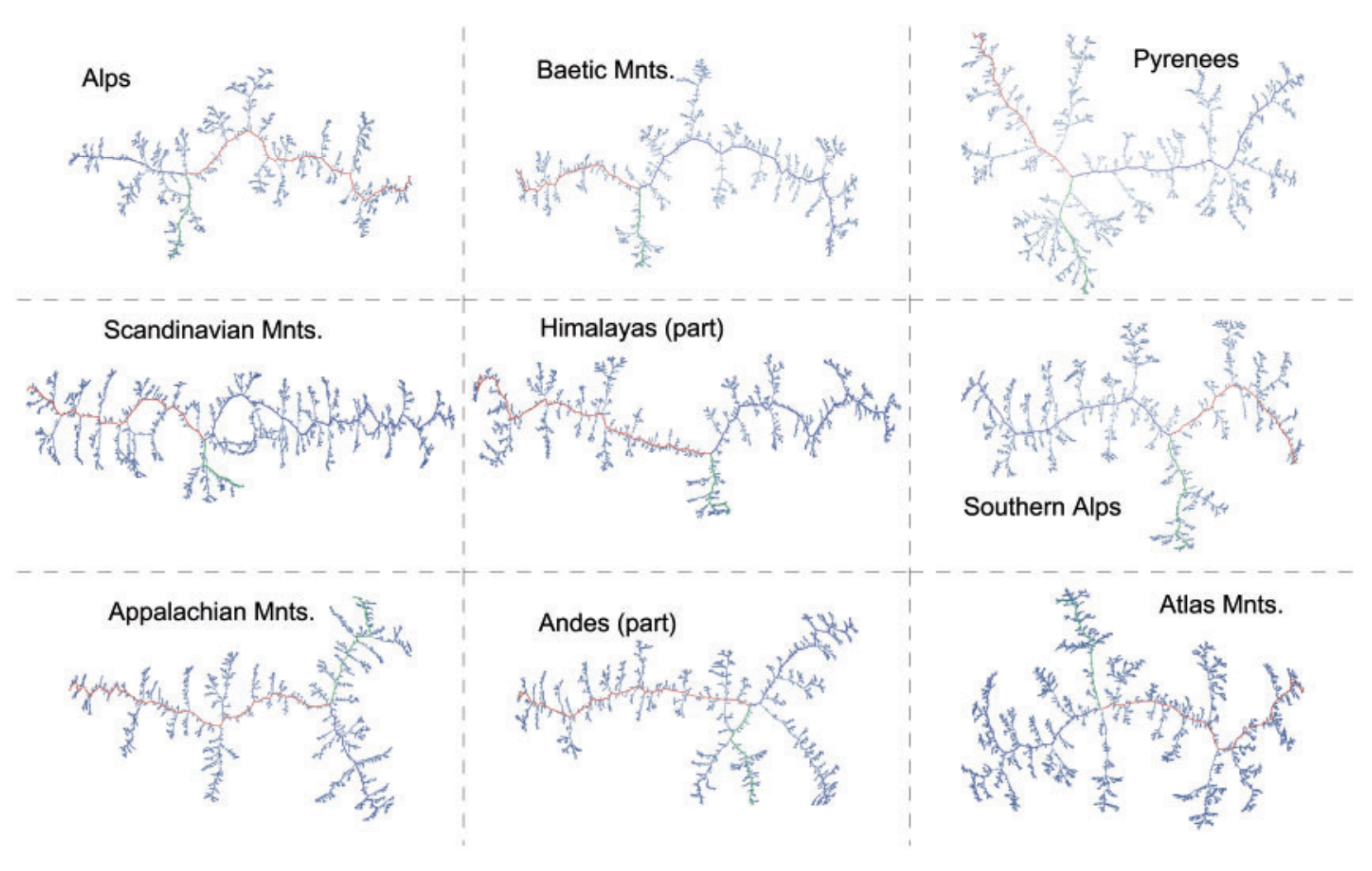
No matter where they appear, or even how, their branched structures share a universal similarity, and that goes for the Alps, the Pyrenees, the Scandinavian Mountains, the Baetic Mountains, the Himalayas, the Andes, the Appalachians, the Atlas Mountains, and the Southern Alps - even though it might not be obvious.
"It would seem that the only thing that the various mountain ranges have in common is that when you look at them, you have to really bend your head back," says researcher Jaroslaw Kwapien from the Institute of Nuclear Physics of the Polish Academy of Sciences (IFJ PAN) in Krakow.
Underneath all that visible diversity, Kwapien and his colleagues noticed something unexpected. On all continents, regardless of how high the peaks, how old the ranges, or whether they were tectonic or volcanic, the results were oddly the same by one measure.
Using topographic maps and fractals, the team investigated mountains' ridge structures and found that the degree of distribution between the 'nodes' - the points at which the ridges branch - turned out to be a power law of nature.
A power law is the relationship between two quantities that change in proportion to each other. For example, if the length of a square doubles in size, the area is multiplied by four.
This phenomenon is found in fractal geometry, and it's used to describe many different aspects of nature, like the branching of trees and river systems, which cluster around a typical value with slight variations.
Mountains are a model example of a natural fractal, so it's no surprise that they follow a power-law topology of ridge graphs. What is surprising, however, is the consistency of values of the power exponent.
"Regardless of the type of mountains, the exponent of the power-law distribution took on values over a very narrow range around the number 5/3," explains Kwapien.
"If we take into account the accuracy of our methodology, this narrow range of values may even mean that the exponents in each examined case were the same."
The observation is counter-intuitive because the topography of the Alps and the Appalachian Mountains differ so much. The first is mainly a system of ridges and valleys, branching out like a neural dendrite. The latter is made up of "long, alternating ridges and valleys with a trellis-like drainage structure".
In spite of their extremely different structures, their highly conserved power-law value implies that the ridge-line structure for any mountain range is universal, and that something else, therefore, must reflect their diversity.
 (IFJ PAN)
(IFJ PAN)
The authors think mountains' similarities arise not due to how they're created, but reflect the existence of river systems, erosion crushing and sculpting, and gravitational landslides, which stay relatively the same in different parts of the world.
"The situation becomes clearer when we consider gravity in addition to water," explains Kwapien.
"When rock material is crushed, it becomes subject to the dynamics of loose bodies regardless of its chemical composition. Loose bodies on slopes can only remain there if the angles of inclination are not too great. The slopes must not be too steep. This is why the depth of valleys in nature is limited by their own width."
The same forces could be a limiting factor for mountain ranges, too, and this begs the question: If different mountain ranges are so similar in terms of size, where are the sources of mountain diversity?
Only more research can say for sure.
The research has been published in the Journal of Complex Networks.
