Magic: The Gathering, the card game where you build your own deck from over 19,000 unique cards and then battle this deck against other people, is not what you would call simple.

But a pre-print paper first published in March turns this already complex game up a notch, showing that a specific set of cards can actually build a Turing machine inside the game.

This machine is a hypothetical device the famous mathematician Alan Turing envisioned in 1936. The original idea features a tape with numbers on it (used in the same way as the memory in a computer), a 'head' to read and edit the tape, and a table of instructions - a 'program' - to tell the head what to do when it reads the number (similar to lines of code).

Although it appears rather simple, the machine can actually simulate the logic of any computer algorithm, no matter how complicated.

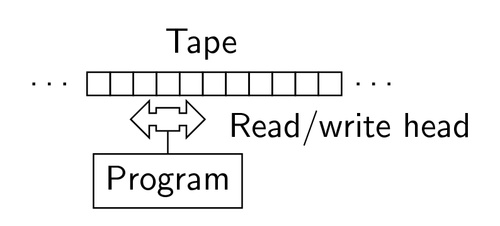turing machine(Ludger Humbert/TEXample/CC BY 2.5)

In the last few years, computer nerds have built versions of the Turing machine out of physical objects and in video games, including this one out of LEGO, and a wild-looking one in the computer game Minecraft.

Now, for the first time, we've got a set of tournament playable cards which - in the perfect combination - can 'summon' a Turing machine in Magic: The Gathering.

In a normal game of Magic, after shuffling your 60-card deck, you pick up the top few cards and choose which ones to use, to cast spells and create things like creatures or enchantments. There are thousands of cards, many of which have different instructions or abilities that 'trigger' when you decide to play them.

For example, some cards let you create creature 'tokens' – while you're only allowed four of one card in one deck, some combinations of cards will trigger the creation of dozens of the same type of creature token. 

The 'Turing machine' deck created by the researchers differs from normal gameplay in that instead of the player deciding which cards to play every time, the optimised deck starts a never-ending cascade of outcomes after a specific set of cards is played: each card in the sequence triggers another one, and another one, and so on.

So, in this scenario, the Turing machine's program is the set of cards, the 'tape' is created by huge numbers of creature tokens on the table, and the 'head' is the player reading the cards and actioning them.

Once this Magic machine gets started, there are two outcomes – either the machine goes on forever in an infinite loop, or it eventually halts – and the player wins.  

The research has been part of a years-long crusade by lead author Alex Churchill, an independent researcher from Cambridge, to find out whether Magic, thanks to its mind-boggling complexity, can be used to build a Turing machine. This website from 2012 shows some of Churchill's early attempts.

So why create a Turing machine inside a card game first released 26 years ago?

Well, the fact that you can do it at all makes Magic truly special amongst table-top games: it means the game possesses a level of complexity known as Turing completeness, a characteristic usually ascribed to programming languages.

Despite how simple the Turing machine might look, any Turing machine can run any algorithm of another Turing machine, including things like computers – although it might take a lot more time - and there's no exception for Magic.

"Literally any function that can be computed by any computer can be computed within a game of Magic," Churchill explains to Jennifer Ouellette at Ars Technica.

But there's another layer here, too.

Generally, most games have a limit on the types of moves and finite actions available (for example, the number of spots on a game board). This makes it easier to work out who will win.

But Magic doesn't have a game board, and there are thousands of card choices you could add to a 60-card deck.

So, if you manage to trigger the correct set of cards with the Turing deck, it's impossible for a computer to know whether you'll end up stopping, or looping forever. This is called the halting problem, and according to the researchers, it's the first time we've seen this in a tabletop game.

"This is the first result showing that there exists a real-world game for which determining the winning strategy is non-computable," the team explains in their paper.

"Magic: The Gathering does not fit assumptions commonly made by computer scientists while modelling games."

So, as fun as this sounds, even if you're an avid Magic player, we wouldn't recommend building this deck and bringing it to a tournament.

All the cards are 'standard' (meaning they're tournament approved), but because decks are shuffled before every game, there's only a 1 in 50,000 chance that the correct string of cards come out to make the Turing machine. Not great odds.

"So I'd need to play about 50,000 games with the deck before I'd draw the perfect hand that allows me to set up the Turing machine," Churchill explains to Ars Technica.

"But if I do, wouldn't that be a story to tell?"

The research has been published in pre-print journal arXiv.