On one level, sudoku is a simple and fun way to pass the time and keep the brain ticking – but dig deeper, and some fiendishly clever math patterns reveal themselves. The most recent to blow our minds? The Phistomefel Ring.
The Phistomefel Ring (or the Phistomefel Theorem) is beautifully illustrated in a video by Numberphile that you'll find embedded below.
It's named after a German sudoku constructor, and as well as being a super-smart pattern of digits, might also help you solve these puzzles more quickly in the future.

If you're new to sudoku – each game board is made up of nine equal squares, each split up into nine smaller squares in a 3 x 3 arrangement. Every row and column on the board, as well as every 3 x 3 square, has to be filled out with the digits 1 to 9, with each digit used only once.
There are more patterns here: every row, column, and 3 x 3 square therefore contains digits that add up to 45, for example. However, Phistomefel found a deeper pattern that's far more impressive.
As per the Phistomefel Ring principle, the 16 squares that circle the central 3 x 3 square will always contain the same digits – in every single sudoku puzzle – as those in the four 2 x 2 squares in the corners of the puzzle board. You can get a better idea of this in the image below:
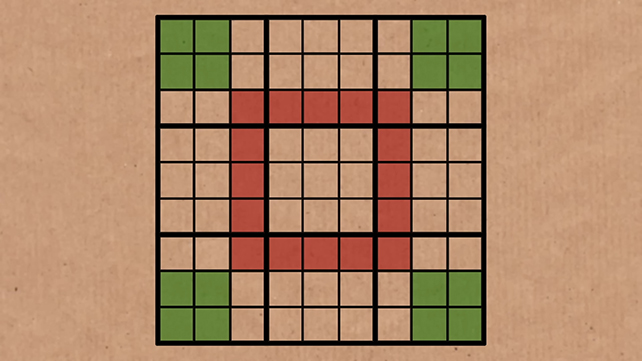
Even though we don't know what order they're in, we do know all the digits in the green squares exactly match all the digits in the red squares. It can take some time to get your head around, but it's beautiful in its symmetry.
The Phistomefel Ring works because of something called Set Equivalence Theory.
Imagine the central column in green and the middle row in red of a sudoku board, overlapping in the middle – the very central square in blue. We know that both the row and the column contain the digits 1 through 9, in whatever order.
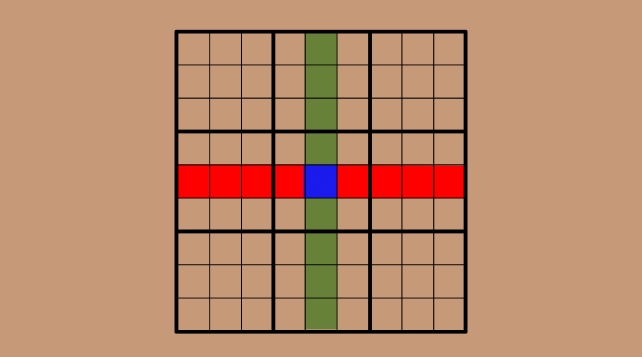
Now, take away the middle blue square, where the overlap is – cutting out the middle of both the row and the column. We don't know what that digit is, but we do know the same digit has been removed from both the row and the column, and the remaining digits will therefore match too.
The Phistomefel Ring is that idea writ large, with eight sets of 1-9 digits rather than just two. There are more numbers involved, but the idea is the same: squares that don't overlap must contain the same digits. You can see the eight sets below, colored in two separate grids:
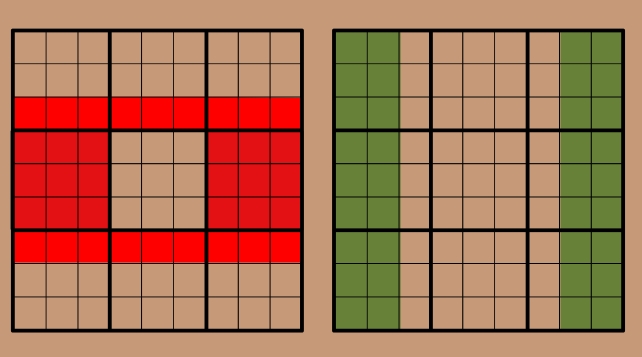
The sets in red are two brightly colored rows, and two 3×3 larger squares on the middle left and middle right of the sudoku grid. The sets in green are in two columns on each side of the grid.
In the next image, the sets are shown on the same grid, with the overlapping squares colored a darker green:
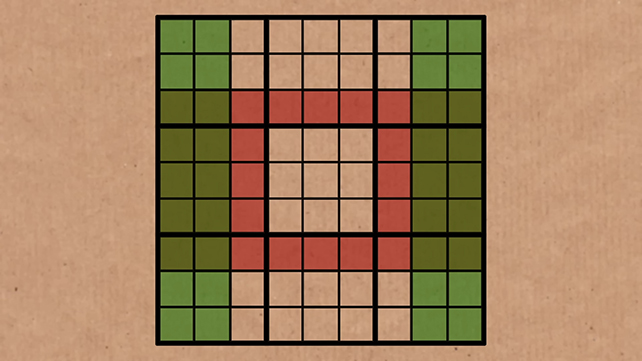
Take away those overlaps, and the remaining blocks in green and red must have the same numbers left over.
Now we're going to see how many more sudoku patterns we can find…
