Most of the laws of physics don't care which direction time is travelling. Forwards, backwards… either way, the laws work exactly the same. Newtonian physics, general relativity - time is irrelevant to the mathematics: This is called time-reversal symmetry.
In the real Universe, things get a bit messier. And now a team of scientists led by astronomer Tjarda Boekholt of the University of Aveiro in Portugal have shown that it takes as few as three gravitationally interacting bodies to break time-reversal symmetry.
"Hitherto, a quantitative relation between chaos in stellar dynamical systems and the level of irreversibility remained undetermined," they wrote in their paper.
"In this work we study chaotic three-body systems in free fall initially using the accurate and precise n-body code Brutus, which goes beyond standard double-precision arithmetic. We demonstrate that the fraction of irreversible solutions decreases as a power law with numerical accuracy."
The n-body problem is a famous problem in astrophysics. It arises as you add more bodies to a gravitationally interacting system.
The movements of two bodies of comparable size in orbit around a central point are relatively simple to mathematically predict, according to Newton's laws of motion and Newton's law of universal gravitation.
However, once you add another body, things become tricky. The bodies start to gravitationally perturb each others' orbits, introducing an element of chaos into the interaction. This means that, although solutions exist for special cases, there is no one formula - under Newtonian physics or general relativity - that describes these interactions with complete accuracy.

Even within the Solar System, which we understand pretty well, we can only predict a few million years into the future. Chaos in the Universe is a feature, not a bug.
When running n-body simulations, physicists sometimes return time-irreversibility in their results - in other words, running the simulations backwards doesn't get them to the original starting point.
What has been unclear is whether this is a result of the chaos of these systems, or problems with the simulations, leading to uncertainty over their reliability.
So, Boekholt and his colleagues designed a test to figure this out. He and computational astrophysicist Simon Portegies Zwart of Leiden University in the Netherlands previously wrote an n-body simulation code called Brutus that uses brute-force computing power to reduce the magnitude of numerical errors.
Now, they have used it to test the time-reversibility of a three-body system.
"Since Newton's equations of motion are time reversible, a forward integration followed by a backward integration of the same time should recover the initial realisation of the system (albeit with a sign difference in the velocities)," they wrote in their paper.
"The outcome of a reversibility test is thus exactly known."
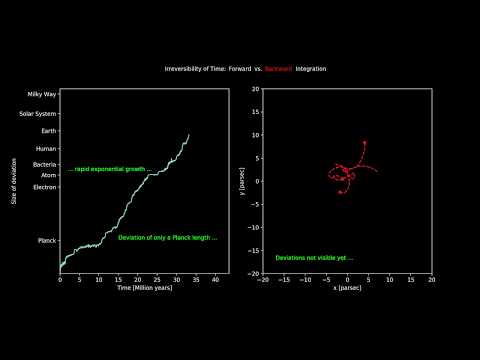
The three bodies in the system are black holes, and they were tested in two scenarios. In the first, the black holes started from rest, moving towards each other into complicated orbits, before one of the black holes is kicked out of the system.
The second scenario starts where the first one ends, and is run backwards in time, trying to restore the system to its initial state.
They found that, 5 percent of the time, the simulation could not be reversed. All it took was a disturbance to the system the size of a Planck length, which, at 0.000000000000000000000000000000000016 metres, is the smallest length possible.
"The movement of the three black holes can be so enormously chaotic that something as small as the Planck length will influence the movements," Boekholt said. "The disturbances the size of the Planck length have an exponential effect and break the time symmetry."
Five percent may not seem like much, but since you can never predict which of your simulations will fall within that five percent, the researchers have concluded that n-body systems are therefore "fundamentally unpredictable".
And they have shown that the problem is not with the simulations after all.
"Not being able to turn back time is no longer just a statistical argument," Portegies Zwart said. "It is already hidden in the basic laws of nature. Not a single system of three moving objects, big or small, planets or black holes, can escape the direction of time."
The research has been published in the Monthly Notices of the Royal Astronomical Society.
