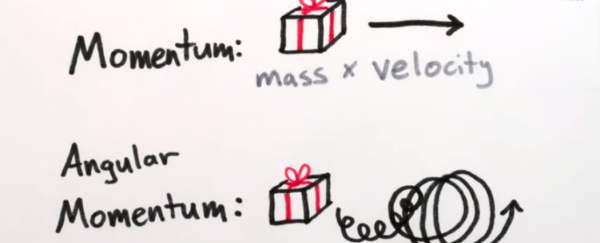When we talk about physics, boiling it right down to its most basic principles, we're really just talking about the motion of the stuff around our Universe. For some objects, this is simple - some move that way, and others move the other way. But what about objects that move without moving? Or, put another way, what about objects that move, but that movement doesn't really take them anywhere, such as a planet around a star, an electron around an atom, and our Solar System going around the gravitational centre of the Milky Way?
So we've got plain old 'momentum', which is mass x velocity, and the 'oomph' an object has when it's going in a straight line; and then we've got 'angular momentum', "which is a way to explain how much oomph objects have when they're going in circles, figuratively or literally," says Henry in the latest episode of MinutePhysics.
The reason we care about angular momentum, he says, is that if you take a bunch of objects that are interacting, for example the Earth orbiting the Sun, you can add up all their angular momenta into one number (don't worry, Henry shows you how to do this in the video above), and then that total value won't change over time. It's a constant. Unless of course, something comes in from outside to mess with the system, but you get the idea.
And here's where it gets mind-blowing. Imagine if we looked at the Earth rotating around the Sun, calculated its angular momentum, and then suddenly took away the Sun and the rest of the Solar System. Turns out, the Earth would still have that same angular momentum about the point where the Sun was, says Henry. Of course, in the absense of the Sun's major gravitational pull, the Earth would now be moving in a straight line, but if you calculate its angular momentum, you're going to end up with the exact same figure that you calculated when the Earth was rotating around the Sun!
Watch the latest episode of MinutePhysics above to find out how you can do these calculations yourself, so you can, well, blow your own mind with physics.
Source: MinutePhysics