Solving one of the oldest algebra problems isn't a bad claim to fame, and it's a claim Norman Wildberger can now make: The mathematician has solved what are known as higher-degree polynomial equations, which have been puzzling experts for nearly 200 years.
Wildberger, from the University of New South Wales (UNSW) in Australia, worked with computer scientist Dean Rubine on a paper that details how these incredibly complex calculations could be worked out.
"This is a dramatic revision of a basic chapter in algebra," says Wildberger. "Our solution reopens a previously closed book in mathematics history."
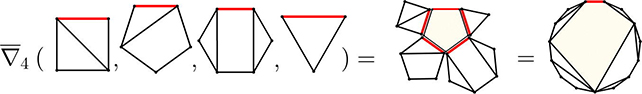
As you might expect, understanding how this works isn't easy for the non-algebra geniuses amongst us. Essentially, polynomials are equations that include variables raised to non-negative powers (e.g. x3). When those powers are five or above, that's a higher-degree polynomial.
Mathematicians have figured out how to solve lower-degree versions, but it was thought that properly calculating the higher-degree ones was impossible. Before this new research, we've been relying on approximations.
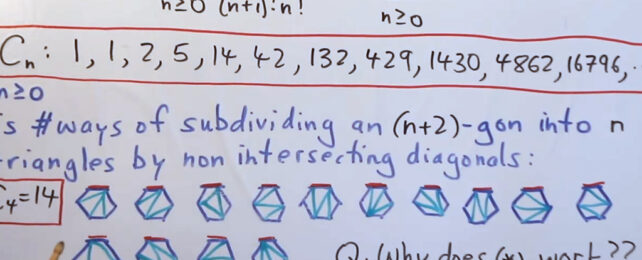
Wildberger and Rubine took a new approach to the problem, which is based on Catalan numbers. These numbers are used in advanced number counting and arrangements, including counting how many ways polygons can be subdivided into triangles.
By extending the idea of Catalan numbers, the researchers were able to demonstrate that they could be used as a basis for solving polynomial equations of any degree. Part of the clever method involved extending polygon counts to other shapes besides triangles.
It's a departure from the traditional method of using radical expressions (like square roots and cube roots) to solve equations like this, instead relying on combinatorics – counting numbers, fundamentally, but in increasingly advanced ways.
"The Catalan numbers are understood to be intimately connected with the quadratic equation," says Wildberger.
"Our innovation lies in the idea that if we want to solve higher equations, we should look for higher analogs of the Catalan numbers."

The researchers put their new algebra up against some well-known polynomial equations of the past, including a famous cubic equation studied by John Wallis. The numbers checked out, validating the new work.
Wildberger and Rubine didn't stop there. They also discovered a new mathematical structure called the Geode, which ties in with Catalan numbers and seems to act as a foundation for them. This Geode could form the basis of many future studies and discoveries, the researchers say.
As the approach taken here is so different to what's gone before, there's the potential to rethink many key ideas that mathematicians have long relied on for computer algorithms, the way data is structured, and game theory. It might even have applications in biology – for counting RNA molecule folding, for example.
"This is a core computation for much of applied mathematics, so this is an opportunity for improving algorithms across a wide range of areas," says Wildberger.
The research has been published in The American Mathematical Monthly.